Sfb 288 Differential Geometry and Quantum Physics

Hierarchical Triangulations 1
n-dimensional Interpolation

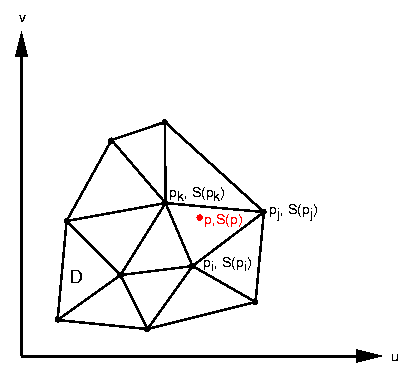
The concept directly extends to n-dimensional parameter spaces D. We tesselate D with n-simplices where each vertex is a keyframe and contains a hierarchy. All key surfaces must fulfil the interpolation condition. In the case n=2 the parameter domain D is a triangulation of the (u,v)-plane. Let p lie in the triangle (p_i, p_j, p_k) with barycentric coordinates (b₁, b₂, b₃). Then the corresponding interpolated surface S(p) can be computed as

S(p) = b₁S(p_i) + b₂S(p_j) + b₃S(p_k)

Author: Axel Friedrich, Konrad Polthier