Sfb 288 Differential Geometry and Quantum Physics

Hierarchical Triangulations 2
1-dimensional Interpolation

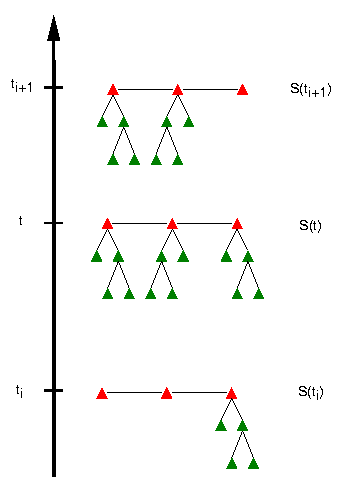
Consider a 1-parameter family (e.g. time-dependent) of surfaces. We discretize the deformation by choosing keyframe surfaces at times (t₁, t₂,...., t_n) and represent each keyframe as a hierarchical triangulation.

We propose the following interpolation condition which will allow interpolation between differently refined keyframes:

All keyframes must have the same number of root nodes.

Then interpolation at time t (t_i <= t <= t_i+1) is performed as follows:

• Compute the union S of the hierarchical triangulations S(t_i ) and S(t_i+1).
• Let (b₁, b₂) be the barycentric coordinates of t in the interval [t_i , t_i+1].
• For each leaf L of S
  • Let L₁, L₂ be the corresponding leaves in S(t_i ) and S(t_i+1).
  • L:=b₁ L₁ + b₂L₂

Author: Axel Friedrich, Konrad Polthier