
|
Sfb 288 Differential Geometry and Quantum Physics
|
 Geodesics and waves
Geodesics and waves
 on piecewise linear surfaces
on piecewise linear surfaces
|
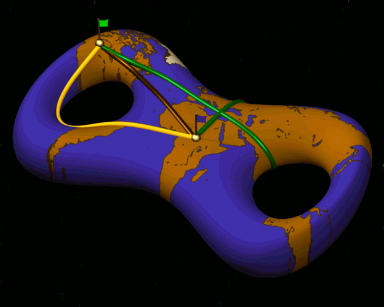
Geodesic curves are a fundamental concept in geodesy and mathematics to
generalize the idea of a "straight line" to curved surfaces and general
manifolds. The straight line property makes them a helpful concept in numerical
methods on arbitrary surfaces and especially discrete surfaces.
|

|
On a piecewise linear surface a discrete geodesic across an edge must have
equal angle on both sides.
|
|
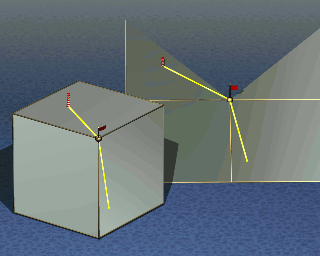
A straightest curve through a vertex of the surface must bisect its total
vertex angle.
|
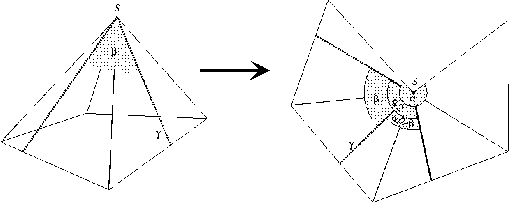

For the numerical integration of a vector field v on a curved surface with
e.g. an Euler Method geodesics may be used in the basic step as follows:

|
From an initial point p proceed a distance h along the geodesic
with initial point p and direction v(p). This avoids ambiguous
projection operations needed in conventional methods.
|
|
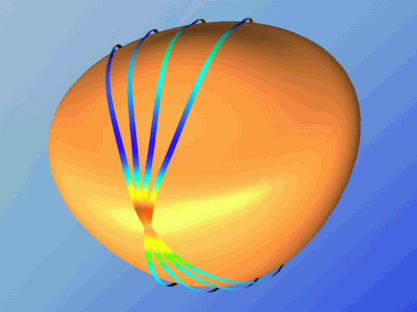
A highly discretised Zoll's Surface with regions of strict negative
curvature. The four discrete geodesics are almost closed. The curvature
of the surface determines its color.
|
An Example: Discrete Geodesics on Zoll's Surfaces
Zoll's surfaces [O.Zoll,1903] have the property that all their geodesics
are simply closed and have same length. They come in a family of rotational
surfaces whose meridians are given as solutions of an ODE. It is remarkable
that the family contains surfaces which have locally strict negative gaussian
curvature. The closedness property of geodesics on a Zoll's suface makes
them suitable candidates for testing the concept of discrete geodesics.
 Author: Konrad Polthier, Markus Schmies
Author: Konrad Polthier, Markus Schmies
Copyright © 1999
Sfb 288,
Mathematics 8-5,
Strasse des 17 Juni 136,
TU-Berlin,
10623
Berlin


 Geodesics and waves
Geodesics and waves
 on piecewise linear surfaces
on piecewise linear surfaces


 Author: Konrad Polthier, Markus Schmies
Author: Konrad Polthier, Markus Schmies