Sfb 288 Differential Geometry and Quantum Physics

Forschungsprogramm des Sfb

Die Grenzen zwischen der Differentialgeometrie und der Mathematischen Physik sind in den letzten Jahren auf vielen Gebieten fließend geworden. Unser Sonderforschungsbereich gibt den Rahmen für eine enge Zusammenarbeit von Mathematikern und Physikern in diesem Bereich. Das folgende Diagramm gibt eine Übersicht über die thematischen Schwerpunkte und deren Querbeziehungen. Hier noch einige Erläuterungen zu den einzelnen Beziehungen (von oben nach unten):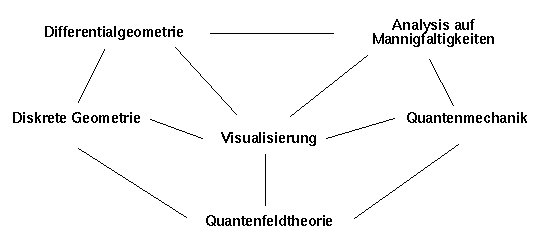

• Eine große Zahl differentialgeometrischer Theorien läßt diskrete (polygonale) Analoga zu, z.B. die Theorie von Flächen im Raum mit konstanter Krümmung. Auch die Beziehungen zur mathematischen Physik über die Theorie integrabler Systeme bleiben diskret bestehen, was zur Entdeckung von neuen diskreten physikalischen Modellen (Felder auf Gittern, Zeit-diskrete Kreisel etc.) führte. Umgekehrt profitiert auch die Differentialgeometrie von ihrer neuen Interpretation als Kontinuumslimes der oft deutlich anschaulicheren diskreten Theorie. Diskrete Geometrie wird in Projektbereich C und A2 studiert, Differentialgeometrie in Teilprojekt A1 und Projektbereich B.

• Die globale Analysis auf Mannigfaltigkeiten und die Beziehung zu deren Geometrie ist Gegenstand von Projektbereich B, sowie der Teilprojekte D6 und D7.

• Die in der Analysis auftretenden Laplace- und Dirac-Operatoren sind auch grundlegend für die in Projektbereich D studierten quantenmechanischen Probleme.

• Computerexperimente und Visualisierung (Teilprojekt A2) sind grundlegend wichtig für alle Themenkreise: Konzepte für numerische Verfahren und für die Visualisierung von differentialgeometrischen Objekten und partiellen Differentialgleichungen auf Mannigfaltigkeiten müssen entwickelt werden. Außerdem müssen Verfahren zur Visualisierung von quantenmechanischen und quantenfeldtheoretischen Modellen gefunden werden. Die in den Projektbereichen C und A2 entwickelten "exakten" Diskretisierungen kontinuierlicher Systeme sind eine wichtige Quelle für neue Algorithmen.

• Kombinatorische Modelle spielen in der Quantenfeldtheorie eine wichtige Rolle, weil hier unter Erhaltung der wesentlichen Struktur die horrenden mathematischen Schwierigkeiten der kontinuierlichen Quantenfeldtheorie wegfallen. Dies ergibt Möglichkeiten der Zusammenarbeit zwischen den Projektbereichen C und F. Die in Projektbereich D unter anderem studierten Vielteilchensysteme liegen an der Grenze der Quantenfeldtheorie