Sfb 288 Differential Geometry and Quantum Physics

Discrete CMC Surfaces
A numerical algorithm

The numerical computation of H-surfaces (H<>0) is faced with stability problems, and standard methods were successful only in few cases. Especially, compact H-surfaces with higher genus have not been computed.

We construct a numerical algorithm based on the definition of a discrete version of the conjugate surface construction of Lawson which great transforms minimal surface in S³ to H=1 surfaces in R³. Here we define discrete harmonic maps from surfaces in S³ to S³, discrete minimal surfaces in S³ (figure below left), and a discrete conjugation algorithm. In the defininition the description of geometric terms as discrete geometric data avoids accumulation of numerical approximation errors.

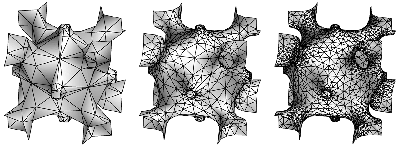
Discrete cmc versions of A.Schoen's O,C-TO surface with 7, 31 and 105 triangles per fundamental patch; the complete cell in a cube consists of 48 fundamental patches. For topological (not numerical) reasons less than 7 triangles seem to be impossible. The algorithm solves a C1 problem for piecewise linear numerical data, and it is an advantage of the discrete techniques that such coarse triangulations suffice.

In the conjugation algorithm we solve a Plateau problem for a discrete minimal surface in S³ by computing a sequence of discrete conjugate maps whose images {Mi} converge to a discrete H-surface in R³. The algorithm made it possible to investigate nummerically compact H-surfaces for the first time.

Lawson's compact minimal surface X2,2 in S3 (stereographically projected to R3) computed with discrete techniques. The symmetry lines on the surface are great circles in S3, they divide the surface into 18 fundamental quadrilaterals with 60 degree angles. The associated constant mean curvature patch can be reflected to the doubly periodic surface on a hexagonal grid which is shown in the background.

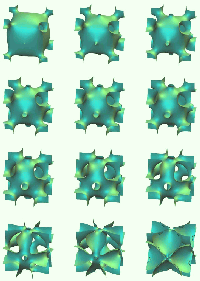
Discrete constant mean curvature companions of A. Schoen's O,C-TO minimal surface. The surface has two free parameters, one controls the distance (which is zero for this sequence) from the top of the handles at the centers of the cubical faces to the outer symmetry planes, the other one controls -- after rescaling the surfaces -- the mean curvature. At both ends of the sequence it is almost one, the O,C-TO minimal surface with zero mean curvature would be in the middle.

Author: B. Oberknapp, K. Polthier