Sfb 288 Differential Geometry and Quantum Physics

Branched texture taps
on arbitrary surfaces

Point waves on surfaces develop singularities at so-called conjugate points. On piecewise linear surfaces they are located at the isolated vertices where all curvature is concentrated. Here the wave branches and the number of layers varies in a neighborhood. Each front of the wave is stored in a separate layer with local support in the texture domain.

Texture maps offer a resolution independent visualization compared to the use of explicitly modelled objects, and have been successfully applied e.g. to the visualization of flows.

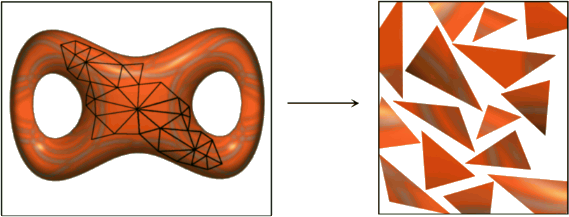
Piecewise isometric texture maps allow 2d-texturing of arbitrary surfaces without distortion effects. Every surface triangle is associated to an isometric planar triangle in the texture domain. Such texture maps are supported by current animation systems.

The visualization of interfering waves on surfaces, evolution of curves, folding of semi-transparent cloth, and branched maps in mathematics require texture domains where the number of texture layers may vary within the surface. We define Branched Texture Maps on arbitary surfaces and apply the concept to branched coverings generated interfering point waves.

Author: Konrad Polthier, Markus Schmies